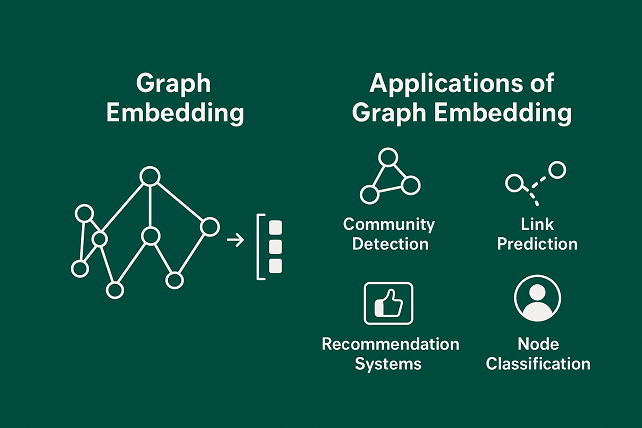
Graph Embedding
Introduction
Graphs are one of the most important data structures used to represent relationships between objects.For example, social networks, transportation systems, or even interactions between proteins can all be modeled as graphs.However, working directly with graphs comes with several challenges:
- Graphs usually have an irregular structure, unlike tabular data or images that have a fixed arrangement.
- Traditional machine learning algorithms are designed for vector-based data, not for graph data
- As a result, applying algorithms directly on graphs is often computationally expensive and complex from a modeling perspective.
This is where Graph Embedding comes into play. In this approach, each node or the entire graph is mapped.to a vector in a continuous vector space. These vectors preserve the essential structural information and relationships of the graph, while making computations much simpler.In simple terms:Graph Embedding means "turning the complex world of graphs into the simple world of numbers," while still keeping the meaning of the connections.
Applications of Graph Embedding
Graph embedding is not just a theoretical concept—it has many practical applications. Some of the most important ones include:
- Community Detection: Identifying groups or clusters in a graph, such as discovering friend groups in social networks.
Link Prediction: Predicting whether a connection between two nodes will form in the future, like friend recommendations in social media.
Recommendation Systems: Leveraging graph structures to suggest content, products, or new connections to users.
Node Classification: Assigning labels or categories to unlabeled nodes, such as identifying user types or the properties of a protein.
Analysis of Complex Networks: Exploring hidden patterns and structures in networks like transportation systems, the internet, or biological networks.
Main Approaches to Garph Embedding
Graph embedding methods can generally be grouped into several main categories:
1. Factorization-based Methods
Idea: Transform the graph into a matrix (e.g., adjacency or similarity matrix) and then factorize it to obtain embeddings.
Examples: Laplacian Eigenmaps, Graph Factorization
Pros: Simple and easy to understand.
Cons: Poor scalability for large graphs.
2. Random Walk-based Methods
Idea: Generate sequences of nodes by performing random walks on the graph, then treat these sequences like sentences (similar to Word2Vec).
Examples: DeepWalk, Node2Vec, LINE
Pros: Scalable and flexible.
Cons: May fail to capture deeper structural information.
3. Neural Network / Deep Learning-based Methods
Idea: Use graph-specific neural networks to learn embeddings.
Examples: Graph Convolutional Networks (GCN), GraphSAGE, Graph Attention Networks (GAT)
Pros: Can capture both local and global features; very powerful in real-world tasks.
Cons: High complexity and requires large amounts of data and computation.
4. Proximity/Similarity Preservation Methods
Idea: Preserve node similarity or proximity in the embedding space (nodes close in the graph should also be close in vector space).
Examples: HOPE (High-Order Proximity preserved Embedding)
Pros: Better at retaining overall graph structure.
5. Graph Autoencoder-based Methods
Idea: Use encoder–decoder architectures to compress and reconstruct the graph.
Examples: GAE, VGAE (Variational Graph AutoEncoder)
Pros: Can model more complex relationships.
Cons: Relatively heavy computation.
Conclusion on Graph Embedding
Graph Embedding is a powerful technique that converts graph data into vector representations that machine learning models can easily process. By doing this, complex tasks such as link prediction, community detection, and recommender systems become faster and more accurate.Different approaches exist—from traditional methods like matrix factorization to modern deep learning models—but all share the same goal: to capture the structure and meaning of graphs in a simpler vector space. In practice, algorithms like Node2Vec and DeepWalk work best for social networks, GCN and GraphSAGE are widely used in biological networks, while methods like LINE or matrix-based models are well suited for information networks.
Comments ( 1 )
Good Article
Post Comment